11  Einführung in die Überlebensanalyse

Die Survival-Analyse ist ein statistisches Verfahren, das sich mit der Analyse der Zeit bis zu einem bestimmten Ereignis, oft als Überlebenszeit bezeichnet, beschäftigt. Solche Ereignisse können unterschiedlich sein, wie z. B. der Tod, das Auftreten einer Krankheit oder das Versagen eines technischen Systems. Wichtige Konzepte sind die Überlebensfunktion, die angibt, wie wahrscheinlich es ist, dass ein Individuum oder Einheit bis zu einem bestimmten Zeitpunkt überlebt, und die Hazardrate, die das instantane Risiko beschreibt, dass das Ereignis zu einem bestimmten Zeitpunkt eintritt. Die Survival-Analyse wird häufig in der Medizin, Biologie und Technik eingesetzt.

11.1 Notation

  • \(\Pr()\): Wahrscheinlichkeit eines Ereignisses
  • \(T\): Überlebenszeit, Time-to-event
  • \(f(t)\): Ereignis- oder Ausfalldichte
  • \(F(t)\): kumulative Verteilungsfunktion
  • \(S(t)\): Überlebensfunktion oder Surivor-Funktion
  • \(h(t)\): Hazard-Funktion, Inzidenzrate, force of transition
  • \(H(t)\): Kumulierte Hazard

11.2 Lernziele

Important

  1. Sie können den Unterschied zwischen Hazard und Survival erklären.

  2. Sie können Sterbetafeln interpretieren.

  3. Sie können mit den Funktionen Surv() und survfit() aus dem Paket survival Überlebenstabellen für eine oder zwei Gruppen erstellen und diese interpretieren.

  4. Sie können die Überlebenskurve für eine oder zwei Gruppen graphisch darstellen.

  5. Sie können mit der Funktion survdiff() prüfen, ob sich die Überlebenskurven von zwei Gruppen statistisch unterscheiden.

11.3 Survivor Funktion

Sei \(T\) eine Zufallsvariable, die die Wartezeit bis zum Eintreten eines Ereignisses darstellt. Die Wahrscheinlichkeit, dass die Überlebenszeit \(T\) kleiner oder gleich \(t\) ist, wird notiert als

\[ F(t) = \Pr(T \leq t). \]

\(F(t)\) stellt die kumulative Verteilungsfunktion von \(T\) dar. \(f(t) = \frac{\mathrm{d}F(t)}{\mathrm{d}t}\) ist die Ereignisdichte. Die Überlebensfunktion \(S(t)\) ist das Komplement von \(F(t)\), also die Wahrscheinlichkeit, dass die Überlebenszeit größer als \(t\) ist: \[ \boxed{S(t) = 1 - F(t) = \Pr(T > t)} \]

11.3.1 Hazard Funktion

Die zentrale Grösse in der Überlebensanalyse ist die hazard function \(h(t)\). Dies stellt eine Inzidenzrate oder force of transition dar. Die Hazard beschreibt den Übergang vom Zustand “lebend” zum Zustand “tot”.

\[ \text{"Lebend"} \boxed{0} \xrightarrow{\color{red}{h(t)}} \boxed{1} \text{"Tot"} \]

Die Hazard ist definiert als: \[ h(t) = \lim_{\Delta t \to 0} \frac{\Pr(t \leq T < t + \Delta t \mid T \geq t)}{\Delta t} \]

Dies stellt die momentane Übergangskraft dar. Hazards sind natürliche Quantitiäten im Umgang mit Time-to-event Daten. Man kann obige Hazard Funktion auch schreiben als Hazard zum Zeitpunkt \(t\) multipliziert mit der Länge eines sehr kleinen Zeitintervalls:

Hazard

\[ h(t) \, \mathrm{d}t = \Pr(T \in \mathrm{d}t \mid {T \geq t}) \]

Das ist Wahrscheinlichkeit, dass ein Ereignis in einem sehr kleinen Zeitintervall d\(t\) eintritt, unter der Bedingung, dass die Person bis kurz vor \(t\) ereignisfrei war.

Die kumulative Hazard ist die integrierte Hazardfunktion, also die kumulierte Hazard über die Zeit: \[ H(t) = \int_0^t h(u) \, \mathrm{d}u \]

Der Anstieg der Hazard zwischen zwei Zeitpunkten \(t_1\) und \(t_2\) ist: \[ \Delta H(t) = H(t_2) - H(t_1) = \int_{t_1}^{t_2} h(u) \, \mathrm{d}u \]

Wenn \(t_1\) nah bei \(t_2\) liegt, dann gilt \(\Delta H(t) \approx h(t) \Delta t\), wobei \(\Delta t = t_2 - t_1\) ist.

11.3.2 Zensierte Daten

Ein fast universelles Merkmal von Überlebensdaten ist die Zensierung. Die häufigste Form ist die Rechtszensierung. Dabei endet der Beobachtungszeitraum oder eine Person wird aus der Studie entfernt, bevor das Ereignis eintritt. Beispielsweise sind manche Personen am Ende einer klinischen Studie noch am Leben oder scheiden aus der Studie aus anderen Gründen als Tod vorzeitig aus. Man kann zeigen, dass zufällige Zensierung die Hazardfunktion nicht beeinflusst.

11.3.3 Zusammenhang zwischen den Größen

Die Hazardfunktion \(h(t)\), die kumulative Hazard \(H(t)\), die Überlebensfunktion \(S(t)\), die Ausfallsdichte \(f(t)\) und die kumulative Ausfallfunktion \(F(t)\) sind miteinander verknüpft (hier ohne Beweise, und wir lernen sie auch nicht auswendig).

Mit diesen Zusammenhängen werden wir im nächsten Abschnitt Beispiele anschauen für verschiedene Hazardfunktionen \(h(t)\).

\[ \begin{align} h(t) &= \frac{f(t)}{S(t)}= -\frac{\mathrm{d}}{\mathrm{d}t} \log S(t)\\ S(t) &= \exp(-H(t))\\ F(t) &= 1 - \exp(-H(t))\\ \log H(t) &= \log (-\log S(t)) \end{align} \]

11.3.4 Konstanter Hazard über die Zeit

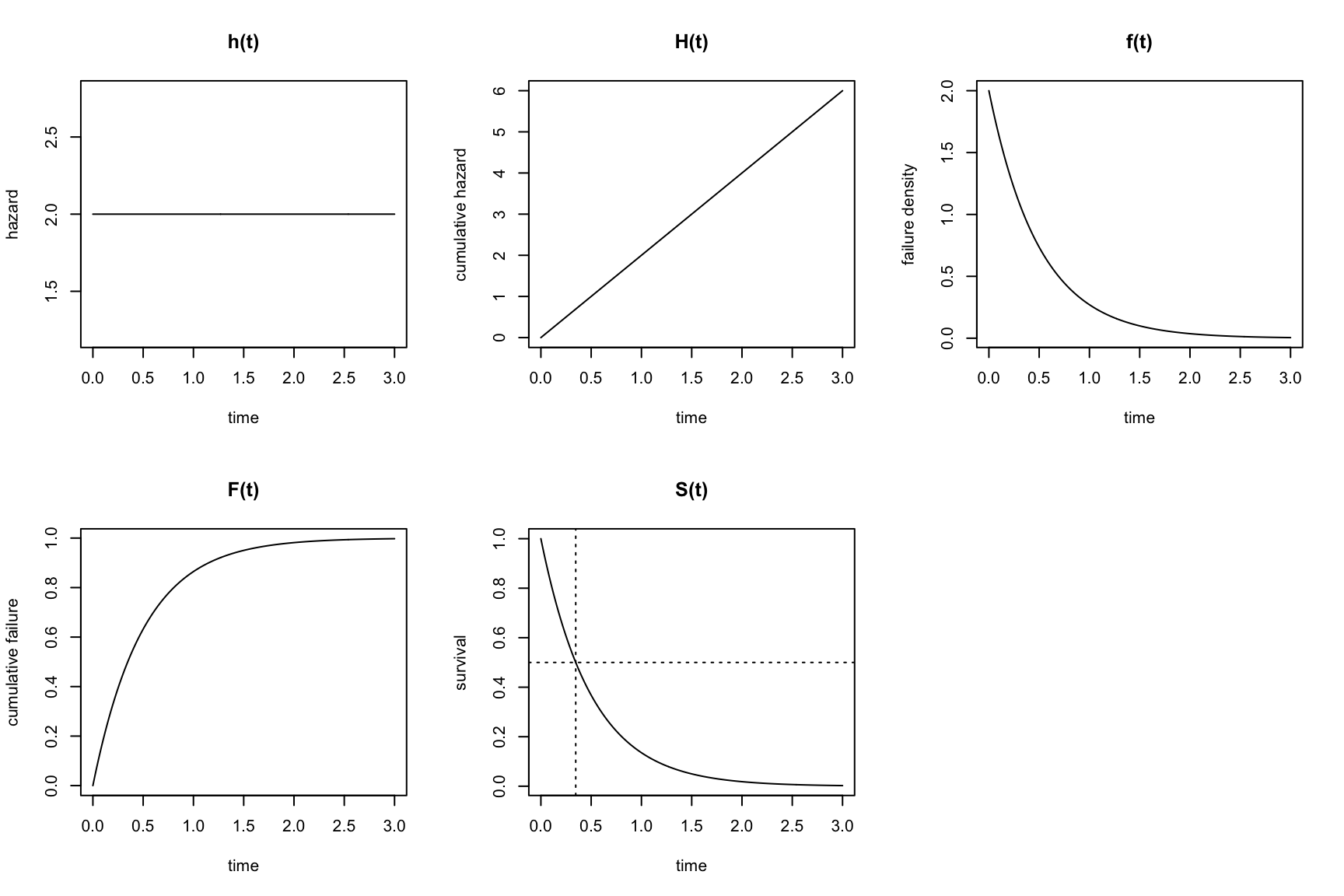
Die einfachste Überlebensverteilung ergibt sich bei konstantem Hazard über die Zeit. Ein Beispiel für konstanten Hazard wäre der Zerfall von radioaktiven Atomen.

  • \(h(t) = \lambda\) ist konstant.
  • \(H(t) = \lambda t\)
  • \(S(t) = \exp(-\lambda t)\).
  • \(F(t) = 1 - \exp(-\lambda t)\).
  • \(f(t) = \lambda \exp(-\lambda t)\).

Nehmen wir \(h(t)=\lambda=2\) als Beispiel. Dies entspricht dann der exponentiellen Verteilung mit (konstanter) Rate \(h=2\). Der Erwartungswert einer Exponentialverteilung ist \(1/h\), hier also 0.5. Der Median einer Exponentialverteilung ist \(\log(2)/h=0.6931472/h=0.3465736\), da \(S(t) = \exp(-\lambda t)=0.5 \Rightarrow t=-\log(0.5)/\lambda \Rightarrow t=\log(2)/\lambda\).

Das entspricht dann der Halbwertszeit, die in der Survivor-Funktion \(S(t)\) sichtbar gemacht wurde.

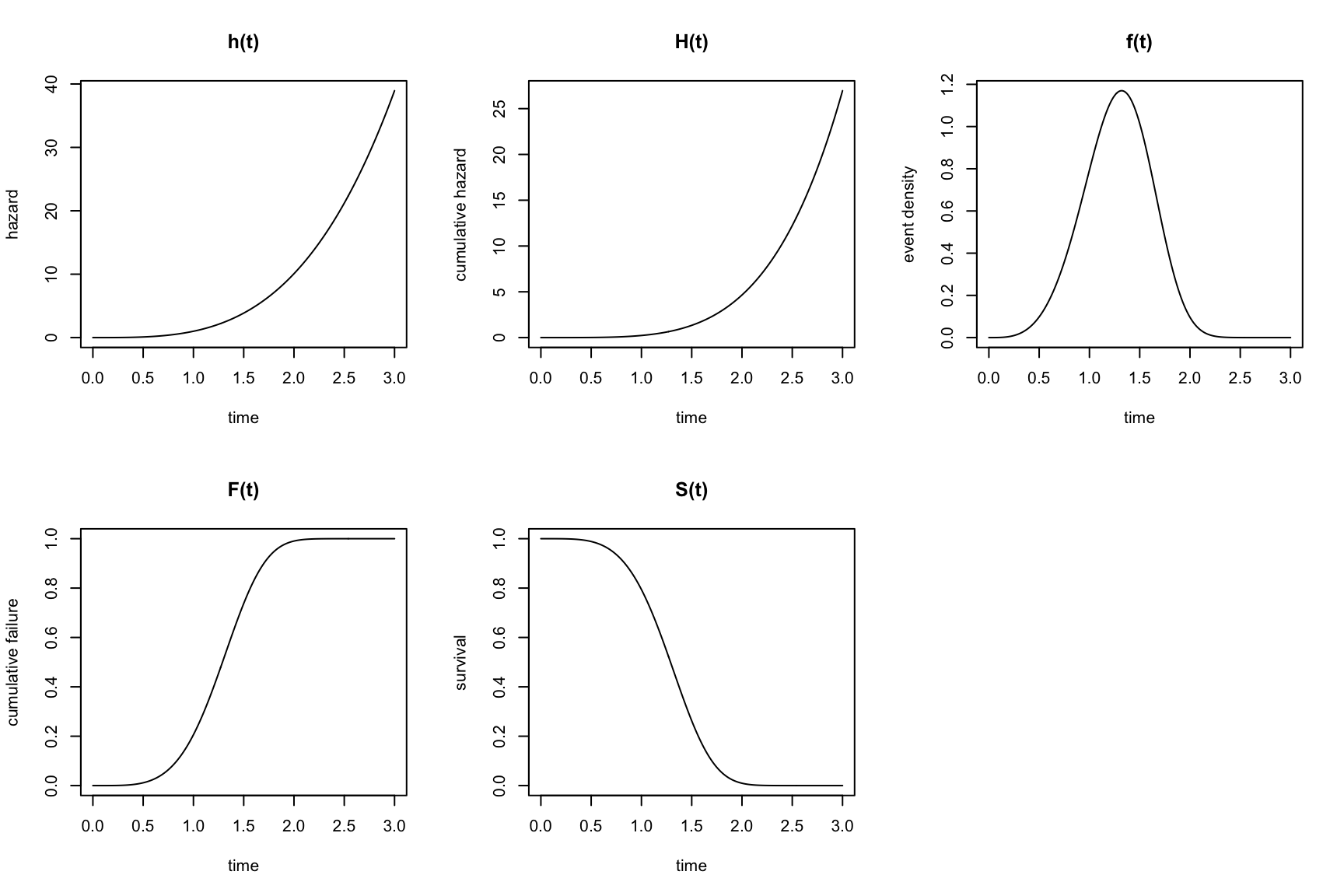
11.3.5 Nicht-konstanter Hazard über die Zeit

In diesem Beispiel betrachten wir eine nicht-konstante Hazardfunktion. Der Hazard hängt also von der Zeit ab: \[ h(t) = t^{\frac{10}{3}} \]

Die folgenden Formeln beschreiben \(h(t), H(t), f(t), F(t)\) und \(S(t)\). Einige erinnern sich vielleicht an die z.T. mühsamen Übungen zum Ableiten und Integrieren an der Mittelschule, wer also Lust hat zum Reproduzieren:

  • \(h(t) = t^{\frac{10}{3}}\)
  • \(H(t) = \frac{3}{13} t^{\frac{13}{3}}\)
  • \(S(t) = \exp\left(-\frac{3}{13} t^{\frac{13}{3}}\right)\)
  • \(f(t) = h(t) \cdot S(t)\)
  • \(F(t) = 1 - S(t)\)

11.4 Schätzung der Überlebensfunktion

Wir haben jetzt die Survivor-Funktion theoretisch eingeführt. Wie immer, brauchen wir ein empirisches Pendant, ein \(\hat{S}(t)\). Dazu gehören im wesentlichen die Sterbetafeln-Methode und der Kaplan-Meier Schätzer.

11.4.1 Sterbetafeln

Die Methode der Sterbetafeln (Life Table Method) ist ein klassischer Ansatz zur Schätzung der Überlebensfunktion \(S(t)\).

Sie basiert auf einer Einteilung der Zeitachse in Intervalle \(i = 1,\dots, I\) von gleicher Länge. Das Sterberisiko \(r_i\) im Intervall \(i\) wird geschätzt als \[ \boxed{\hat{r}_i = \frac{\text{Anzahl der Patienten, die im Intervall } i \text{ gestorben sind}}{\text{Anzahl der Patienten, die zu Beginn des Intervalls } i \text{ noch lebten}} = \frac{d_i}{n_i}.} \]

Die Überlebensfunktion wird dann geschätzt als: \[ \boxed{\hat{S}(t) = \prod_{i=1}^t (1 - \hat{r}_i) = (1 - \hat{r}_1) \times \dots \times (1 - \hat{r}_t)} \]

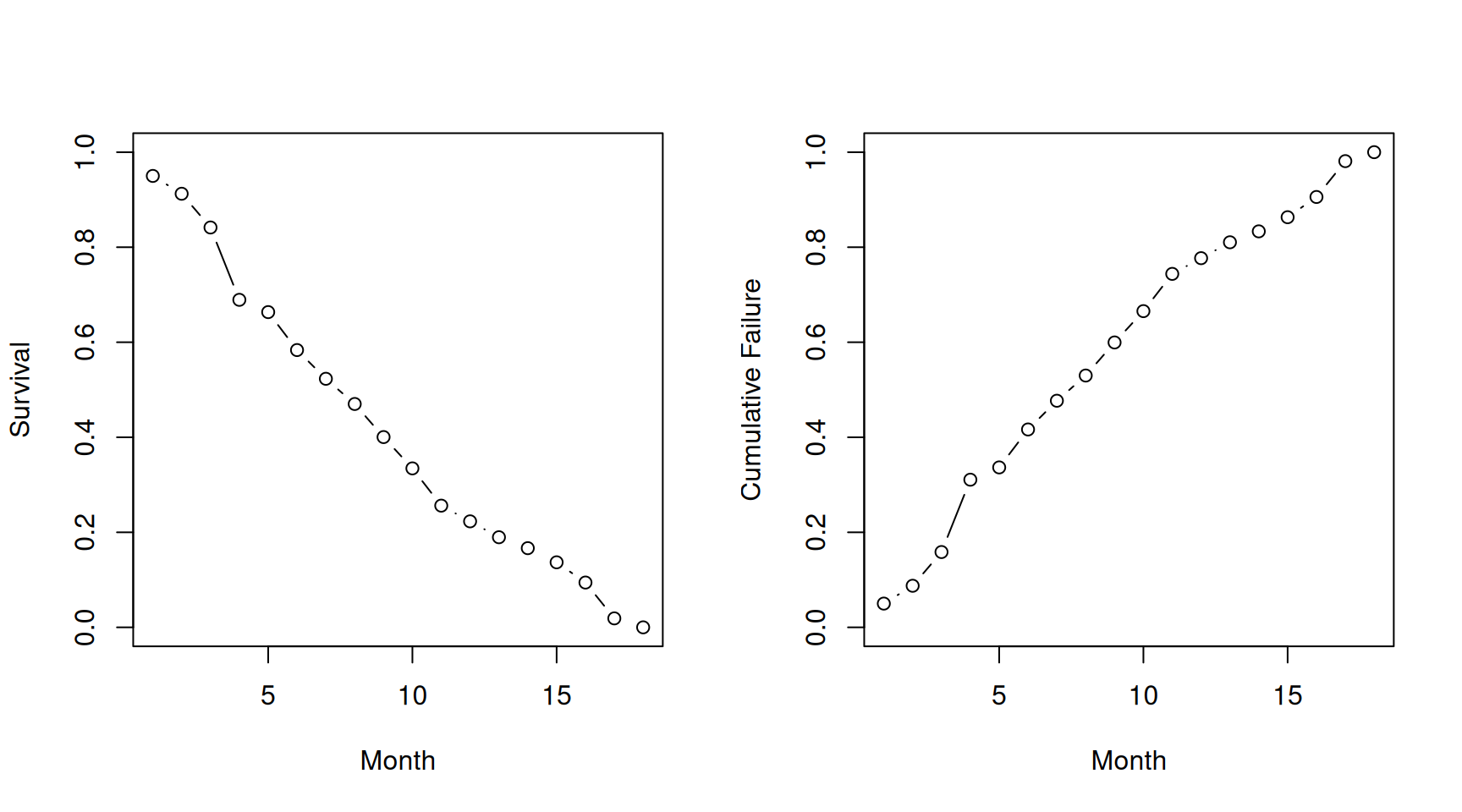
Versuche, die Werte in Tabelle 11.1 nachzuvollziehen. Eine Nuance ist, dass die “At risk”-Anzahl alle Überlebenden am Beginn des Intervals minus 0.5 der zensierten Fälle darstellt.

Tabelle 11.1: Life Table
Month AliveBegin Deaths Censored AtRisk RiskDeath RiskSurv Survival
1 240 12 0 240.0 0.0500000 0.9500000 0.9500000
2 228 9 0 228.0 0.0394737 0.9605263 0.9125000
3 219 17 1 218.5 0.0778032 0.9221968 0.8415046
4 201 36 4 199.0 0.1809045 0.8190955 0.6892726
5 161 6 2 160.0 0.0375000 0.9625000 0.6634249
6 153 18 7 149.5 0.1204013 0.8795987 0.5835476
7 128 13 5 125.5 0.1035857 0.8964143 0.5231005
8 110 11 3 108.5 0.1013825 0.8986175 0.4700672
9 96 14 3 94.5 0.1481481 0.8518519 0.4004276
10 79 13 0 79.0 0.1645570 0.8354430 0.3345345
11 66 15 4 64.0 0.2343750 0.7656250 0.2561280
12 47 6 1 46.5 0.1290323 0.8709677 0.2230792
13 40 6 0 40.0 0.1500000 0.8500000 0.1896173
14 34 4 2 33.0 0.1212121 0.8787879 0.1666334
15 28 5 0 28.0 0.1785714 0.8214286 0.1368774
16 23 7 1 22.5 0.3111111 0.6888889 0.0942933
17 15 12 0 15.0 0.8000000 0.2000000 0.0188587
18 3 3 0 3.0 1.0000000 0.0000000 0.0000000

Die geschätzte Survival \(\hat{S}(t)\) und Kumulative Failure \(\hat{F}(t)\) können wir plotten:

11.4.2 Kaplan-Meier-Schätzer

In vielen Studien ist die exakte Nachbeobachtungszeit für jedes Individuum bekannt, sodass eine Aggregation in beliebigen Zeitintervallen vermieden werden kann. Der Kaplan-Meier-Schätzer der Überlebensfunktion nutzt Intervalle, die nur ein Ereignis enthalten. Die Anwendung der Lebenszeittabellen-Methode auf diese Intervalle liefert im Wesentlichen den Kaplan-Meier-Schätzer.

Die NCCTG-Lungendaten betreffen das Überleben von Patienten mit fortgeschrittenem Lungenkrebs, gesammelt von der North Central Cancer Treatment Group. Die Leistungspunkte bewerten, wie gut der Patient alltägliche Aktivitäten ausführen kann. Siehe für Code-Book ?survival::lung.

library(survival)
  • inst: Institution
  • time: Survival time in days
  • status: censoring status 1=censored, 2=dead
  • age: Age in years
  • sex: Male=1 Female=2
  • ph.ecog: ECOG performance score as rated by the physician. 0=asymptomatic, 1= symptomatic but completely ambulatory, 2= in bed <50% of the day, 3= in bed > 50% of the day but not bedbound, 4 = bedbound
  • ph.karno: Karnofsky performance score (bad=0-good=100) rated by physician
  • pat.karno: Karnofsky performance score as rated by patient
  • meal.cal: Calories consumed at meals
  • wt.loss: Weight loss in last six months (pounds)
lung$sex<-factor(lung$sex,levels=c(1,2),labels=c("m","f"))
str(lung)
'data.frame':   228 obs. of  10 variables:
 $ inst     : num  3 3 3 5 1 12 7 11 1 7 ...
 $ time     : num  306 455 1010 210 883 ...
 $ status   : num  2 2 1 2 2 1 2 2 2 2 ...
 $ age      : num  74 68 56 57 60 74 68 71 53 61 ...
 $ sex      : Factor w/ 2 levels "m","f": 1 1 1 1 1 1 2 2 1 1 ...
 $ ph.ecog  : num  1 0 0 1 0 1 2 2 1 2 ...
 $ ph.karno : num  90 90 90 90 100 50 70 60 70 70 ...
 $ pat.karno: num  100 90 90 60 90 80 60 80 80 70 ...
 $ meal.cal : num  1175 1225 NA 1150 NA ...
 $ wt.loss  : num  NA 15 15 11 0 0 10 1 16 34 ...

Schauen wir uns die Daten an:

psych::headTail(lung)
    inst time status age  sex ph.ecog ph.karno pat.karno meal.cal wt.loss
1      3  306      2  74    m       1       90       100     1175    <NA>
2      3  455      2  68    m       0       90        90     1225      15
3      3 1010      1  56    m       0       90        90     <NA>      15
4      5  210      2  57    m       1       90        60     1150      11
...  ...  ...    ... ... <NA>     ...      ...       ...      ...     ...
225   13  191      1  39    m       0       90        90     2350      -5
226   32  105      1  75    f       2       60        70     1025       5
227    6  174      1  66    m       1       90       100     1075       1
228   22  177      1  58    f       1       80        90     1060       0

Wir kreieren ein survival Objekt mit Surv():

S<-with(lung,Surv(time,status))
S
  [1]  306   455  1010+  210   883  1022+  310   361   218   166   170   654 
 [13]  728    71   567   144   613   707    61    88   301    81   624   371 
 [25]  394   520   574   118   390    12   473    26   533   107    53   122 
 [37]  814   965+   93   731   460   153   433   145   583    95   303   519 
 [49]  643   765   735   189    53   246   689    65     5   132   687   345 
 [61]  444   223   175    60   163    65   208   821+  428   230   840+  305 
 [73]   11   132   226   426   705   363    11   176   791    95   196+  167 
 [85]  806+  284   641   147   740+  163   655   239    88   245   588+   30 
 [97]  179   310   477   166   559+  450   364   107   177   156   529+   11 
[109]  429   351    15   181   283   201   524    13   212   524   288   363 
[121]  442   199   550    54   558   207    92    60   551+  543+  293   202 
[133]  353   511+  267   511+  371   387   457   337   201   404+  222    62 
[145]  458+  356+  353   163    31   340   229   444+  315+  182   156   329 
[157]  364+  291   179   376+  384+  268   292+  142   413+  266+  194   320 
[169]  181   285   301+  348   197   382+  303+  296+  180   186   145   269+
[181]  300+  284+  350   272+  292+  332+  285   259+  110   286   270    81 
[193]  131   225+  269   225+  243+  279+  276+  135    79    59   240+  202+
[205]  235+  105   224+  239   237+  173+  252+  221+  185+   92+   13   222+
[217]  192+  183   211+  175+  197+  203+  116   188+  191+  105+  174+  177+

Wir sehen die Zeiten beim Ereignis. Die \(+\) weisen auf zensierte Zeiten hin. Das sind Zeitpunkte, in denen eine Person die Studie ohne Eintreffen vom Ereignis verlässt oder die Studie beendet war, ohne dass das Ereignis eingetroffen ist.

Nun die Kaplan-Meier Schätzung vom Survival. Diese bekommen wir mit survfit(),

m.km<-survfit(S~1)

Hier schreiben wir ~1, (one-sample), da wir keine kategorielle Eingangsgrösse haben. Die Anzahl Events sowie Median-Survival mit 95% KI bekommen wir mit

m.km
Call: survfit(formula = S ~ 1)

       n events median 0.95LCL 0.95UCL
[1,] 228    165    310     285     363

Mit summary(m.km) bekommen wir die Kaplan-Meier Tabelle. Da diese lang ist, hier nur die ersten 10 Zeilen:

   time n.risk n.event n.censor      surv
1     5    228       1        0 0.9956140
2    11    227       3        0 0.9824561
3    12    224       1        0 0.9780702
4    13    223       2        0 0.9692982
5    15    221       1        0 0.9649123
6    26    220       1        0 0.9605263
7    30    219       1        0 0.9561404
8    31    218       1        0 0.9517544
9    53    217       2        0 0.9429825
10   54    215       1        0 0.9385965

Wir können die Survival oder Failure plotten mit

par(mfrow=c(1,2))
plot(m.km, xlab = "time", ylab = "Survival")# default
plot(m.km, fun = "F", xlab = "time", ylab = "Cumulative failure")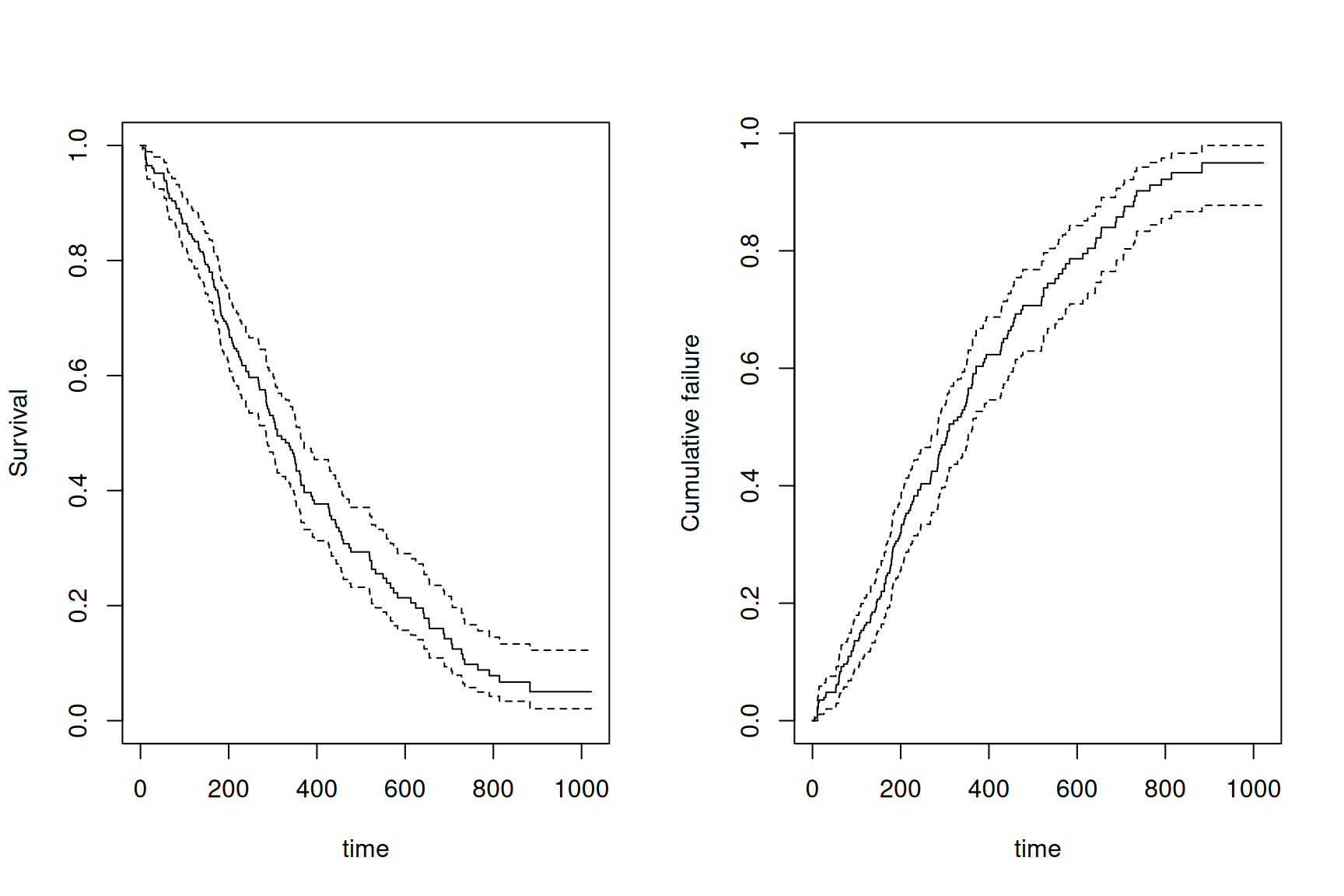

11.4.3 Zwei Gruppen vergleichen

Oft wollen wir zwei Survival-Funktionen vergleichen, hier zum Beispiel bezüglich biologischem Geschlecht. Diese ist jetzt ein unabhängiger kategorieller Prädiktor:

m.km2<-survfit(Surv(time,status)~sex,data=lung)
m.km2
Call: survfit(formula = Surv(time, status) ~ sex, data = lung)

        n events median 0.95LCL 0.95UCL
sex=m 138    112    270     212     310
sex=f  90     53    426     348     550

Schauen wir und die beiden Survival-Funktionen an (mit Intervallschätzung)

par(mfrow=c(1,2))
plot(m.km2, lty = 1:2,col=1:2)
legend(600, 0.9, c("m", "f"), lty =1:2,col=1:2)
title("Kaplan-Meier Curves")
plot(m.km2, lty = 1:2, col=1:2,conf.int = 0.95,xlab="days",ylab="survival")
legend(600, 0.9, c("m", "f"), lty = 1:2,col= 1:2)
title("Kaplan-Meier Curves")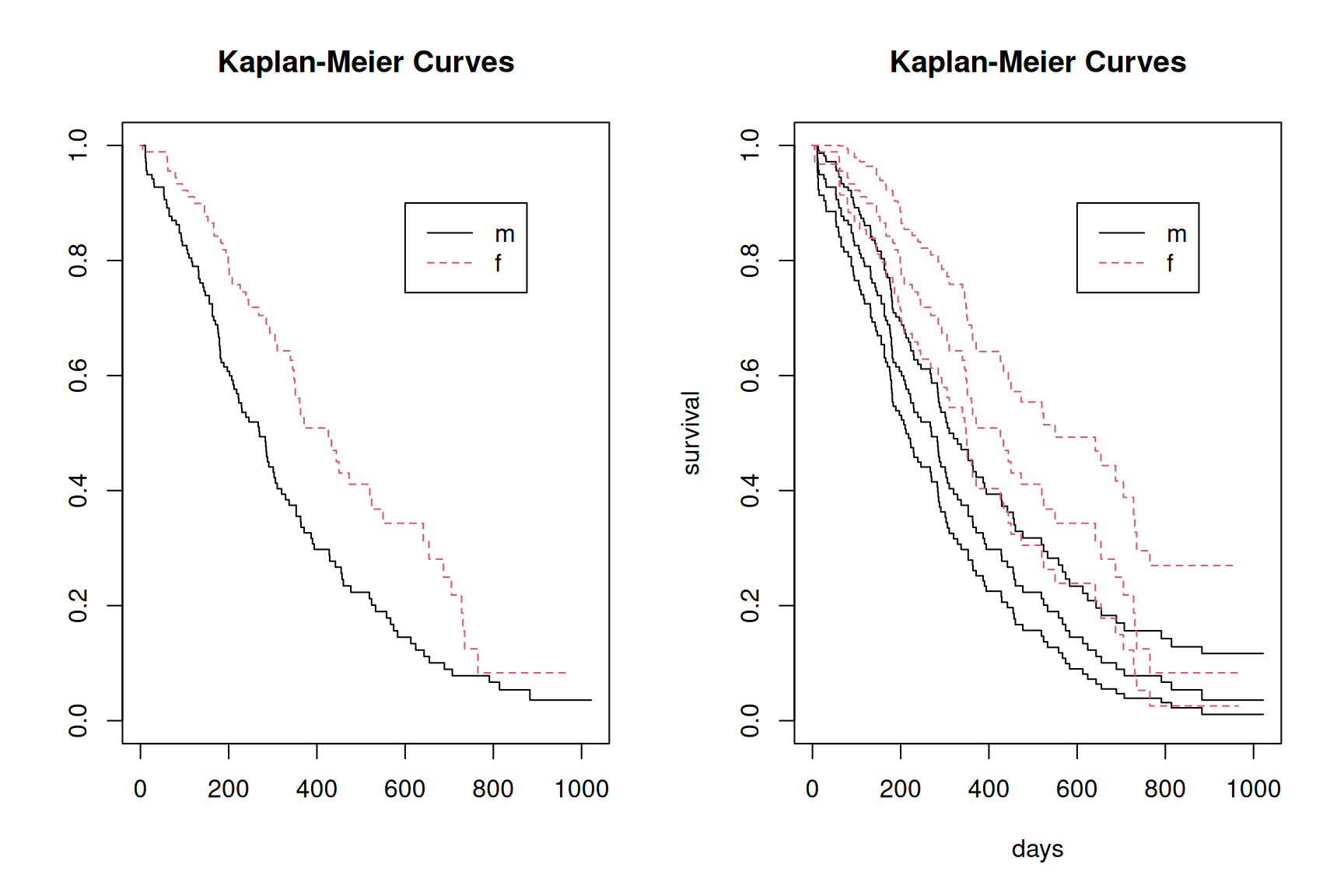

11.4.4 Log-Rank-Test

Der Log-Rank-Test ist ein statistisches Verfahren, das verwendet wird, um zu prüfen, ob es signifikante Unterschiede zwischen zwei oder mehr Überlebenskurven gibt. Dieser Test ist besonders nützlich in der medizinischen Forschung, um zu analysieren, wie verschiedene Behandlungen oder Risikofaktoren das Überleben von Patienten beeinflussen. Dabei vergleicht der Log-Rank-Test die beobachteten und erwarteten Ereignisse (z. B. Todesfälle) in den verschiedenen Gruppen über die Zeit hinweg, um festzustellen, ob die Unterschiede statistisch signifikant sind.

Den Log-Rank Test bekommen wir mit survdiff():

survdiff(Surv(time,status)~sex,data=lung)
Call:
survdiff(formula = Surv(time, status) ~ sex, data = lung)

        N Observed Expected (O-E)^2/E (O-E)^2/V
sex=m 138      112     91.6      4.55      10.3
sex=f  90       53     73.4      5.68      10.3

 Chisq= 10.3  on 1 degrees of freedom, p= 0.001

Die Nullhyothese, dass sich die Überlebenskurven der beiden Gruppen nicht unterscheiden, würde also verworfen.

Es gibt immer viele Alternativen fürs Plotten, z.B. eine Funktion aus dem Paket survminer:

survminer::ggsurvplot(m.km2, data = lung, conf.int = TRUE, surv.median.line = "hv", legend.labs = c("m", "f"), pval = TRUE)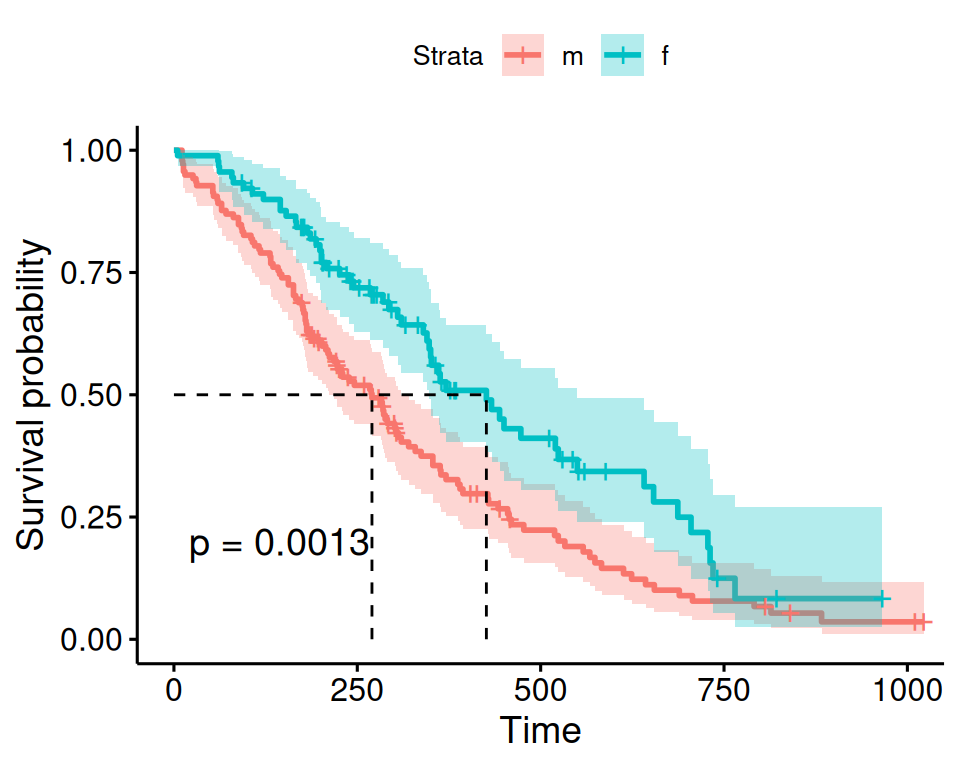

Hier sind die beiden Median-Survivals dargestellt.

11.5 Exkurs: Modelle für Überlebensdaten

Das Cox-Regressionmodell für proportionale Hazardraten ist das gebräuchlichste Werkzeug zur Untersuchung der Abhängigkeit der Überlebenszeit von kategoriellen und kontinuierlichen Prädiktorvariablen. Seien \(h_1(t)\) und \(h_2(t)\) die Hazardfunktionen in zwei Gruppen. Die proportionale Hazardannahme impliziert, dass \[ \frac{h_1(t)}{h_2(t)}=\text{konstant}. \]

Das Cox-Modell ist semi-parametrisch und ist das am meisten gebrauchte Modell bei Time-to-Event Daten.

11.5.1 Cox-Regressionmodell für proportionale Hazardraten

Für jede Einheit \(i\) kann die Hazardrate nun von Kovariaten \(x_1,\dots, x_m\) abhängen. Das Modell wird geschrieben als

\[ h_i(t)=h_0(t)\cdot\exp(\beta_1x_{i1}+\dots +\beta_mx_{im}), \quad i=1,\ldots,n, \]

oder (die \(\log\)-Regel verfolgt uns auf Schritt und Tritt…)

\[ \boxed{\log (h_i(t))=\underbrace{\log (h_0(t))}_{\text{"Intercept"}}+\beta_1x_{i1}+\dots +\beta_mx_{im}, \quad i=1,\ldots,n,} \]

mit einer nicht spezifizierten Basis-Hazardfunktion \(h_0(t)\), einem \(m\)-Vektor von Regressionskoeffizienten und einem \(m\)-Vektor von Kovariaten. Das Ziel ist dann, den Effekt von Eingangsgrössen auf die Hazardrate zu schätzen.

Wenn wir zwei Einheiten \(1\) und \(2\) mit Hazard \(h_1\) und \(h_2\) vergleichen, haben wir

\[\begin{align} \frac{h_1(t)}{h_2(t)}&=\frac{\exp(\beta_1x_{11}+\dots+\beta_mx_{1m})}{\exp(\beta_1x_{21}+\dots+ \beta_mx_{2m})}\\ &=\exp((\beta_1x_{11}+\dots +\beta_mx_{1m})-(\beta_1x_{21}+\dots+ \beta_mx_{2m}))\\ &=\exp(\beta_1(x_{11}-x_{21})+\dots +\beta_m(x_{1m}-x_{2m})), \end{align}\]

und

\[ \log \frac{h_1(t)}{h_2(t)}=\beta_1(x_{11}-x_{21})+\dots +\beta_m(x_{1m}-x_{2m}). \]

Die Größen \(\beta_k\) reflektieren also den Effekt einer Erhöhung der Kovariate \(x_k\) um eine Einheit (andere Eingangsgrössen konstant gehalten) und können als Log Hazard Ratios (HR) interpretiert werden. Die Größen \(\exp(\beta_k)\) reflektieren den Effekt einer Erhöhung der Kovariate \(x_k\) um eine Einheit (andere Eingangsgrössen konstant gehalten) und können als Hazard Ratios (HR) interpretiert werden.

Wir haben oben die KM-Kurven für zwei Gruppen verglichen. Wir hatten dann nur einen kategorischen Prädiktor. Die alternative Analyse wäre ein Anpassen eines Cox-Models mit coxph():

m.cox1 <- coxph(Surv(time, status) ~ sex, data = lung)
summary(m.cox1)
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)

  n= 228, number of events= 165 

        coef exp(coef) se(coef)      z Pr(>|z|)   
sexf -0.5310    0.5880   0.1672 -3.176  0.00149 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

     exp(coef) exp(-coef) lower .95 upper .95
sexf     0.588      1.701    0.4237     0.816

Concordance= 0.579  (se = 0.021 )
Likelihood ratio test= 10.63  on 1 df,   p=0.001
Wald test            = 10.09  on 1 df,   p=0.001
Score (logrank) test = 10.33  on 1 df,   p=0.001

Wir erkennen im Output obigen Log-Rank-Test, einen Score-Test. Hier werden alle drei Tests gemacht, die wir im Zusammenhang mit der Likelihood-Inferenz eingeführt haben. Alle Tests sind praktisch äquivalent.

Die geschätzte Hazard-Ratio ist 0.5880028. Die Hazard, die force of transition ist für Männer um den Faktor 1.7006721 grösser als bei Frauen und das diesbezügliche Konfidenzintervall überdeckt den Nulleffekt (\(H_0: \log HR=0\) oder \(HR=1\)) nicht.

Auch hier können wir zusätzliche kategorielle oder kontinuierliche Prädiktoren ins Modell aufnehmen. Wenn wir für age korrigieren, ändern sich der Effekt von sex nicht substantiell. age konfundiert den sex Effekt auf survival nicht.

m.cox <- coxph(Surv(time, status) ~ sex+age, data = lung)
summary(m.cox)
Call:
coxph(formula = Surv(time, status) ~ sex + age, data = lung)

  n= 228, number of events= 165 

          coef exp(coef)  se(coef)      z Pr(>|z|)   
sexf -0.513219  0.598566  0.167458 -3.065  0.00218 **
age   0.017045  1.017191  0.009223  1.848  0.06459 . 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

     exp(coef) exp(-coef) lower .95 upper .95
sexf    0.5986     1.6707    0.4311    0.8311
age     1.0172     0.9831    0.9990    1.0357

Concordance= 0.603  (se = 0.025 )
Likelihood ratio test= 14.12  on 2 df,   p=9e-04
Wald test            = 13.47  on 2 df,   p=0.001
Score (logrank) test = 13.72  on 2 df,   p=0.001